In economics, a production function represents the relationship between the output and the combination of factors, or inputs, used to obtain it.
Q=f(L,K)
Where:
- Q is the quantity of products
- L the quantity of labor applied to the production of Q, for example, hours of labor in a month.
- K the hours of capital applied to the production of Q, for example, hours a machine has been working for the production of Q.
There can be other inputs, K and L are just examples.
The Cobb-Douglas production function is a particular form of the production function. It is widely used because it has many attractive characteristics, as we will see below.
The basic form of the Cobb-Douglas production function is as follows:
Q(L,K) = A Lβ Kα
Where:
- Q is the quantity of products.
- L is the quantity of labor.
- K is the quantity of capital.
- A is a positive constant.
- β and α are constants between 0 and 1.
Graphically:

Marginal Product
Marginal product is the change in total production, when there is an infinitesimal change in the inputs. Marginal product is the first derivative of the production function with respect to an input.
∂Q/∂L
In the case of the Cobb-Douglas production function:
∂Q/∂L = Aβ L(β-1) Kα
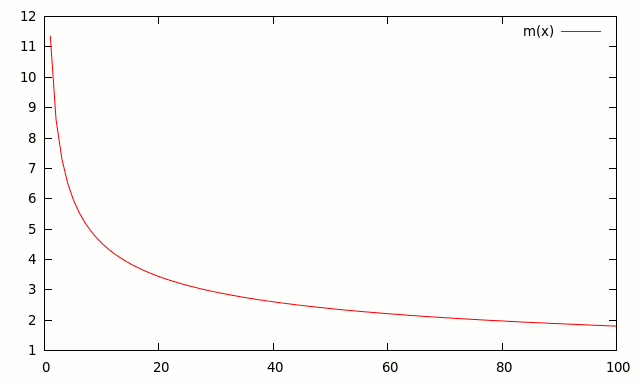
We can see that if L or K increases, the total output will increase, that is, the marginal product is positive.
As we can see in the following plots, the marginal product is decreasing.

Output Elasticity
Output elasticity is the porcentual change in output in respond to a change in levels of either labor or capital.
(∂Q/Q) / (∂L/L) = (∂Q/∂L) / (Q/L)
If output elasticity is greater than 1, the production function is elastic and vice versa. In the case of the Cobb-Douglas production function, output elasticity can be measured quite easily:
(∂Q/Q) / (∂L/L) = (∂Q/∂L) / (Q/L)
= [ Aβ L(β-1) Kα ] / [ A Lβ Kα / L ]
= [ Aβ L(β-1) Kα ] / [ A L(β-1) Kα ]
= β
Output elasticity with respect to labor is constant and equal to β. If β is 0.2 and labor increases in 10%, output will increase 2%.
α and β are output elasticities of capital and labor, and are constant.
Returns to scale
Returns to scale measure how much additional output will be obtained when all factors change proportionally. If the output increases more than proportionally, we say we have increasing returns to scale. If the output increases less than proportionally, we say we have decreasing returns to scale.
In the case of the Cobb-Douglas production function, to check how much will output increase when all factors increase proportionally, we multiply all inputs by a constant factor c. Y’ represents the new output level.
Y’ = A (cL)β (cK)α
= A cβ Lβ cα Lα
= cβ cα A Lβ Kα
= c(β+α) Y
As we can see, if all inputs change by a factor of c, output increases by c(β+α).
Then:
If β+α=1 , the production function has constant returns to scale.
If β+α > 1 , the production function has increasing returns to scale.
If β+α < 1 , the production function has decreasing returns to scale.



